Computing size integrals

Jaideep Joshi

11 March 2022

Developer notes for computing the size integral

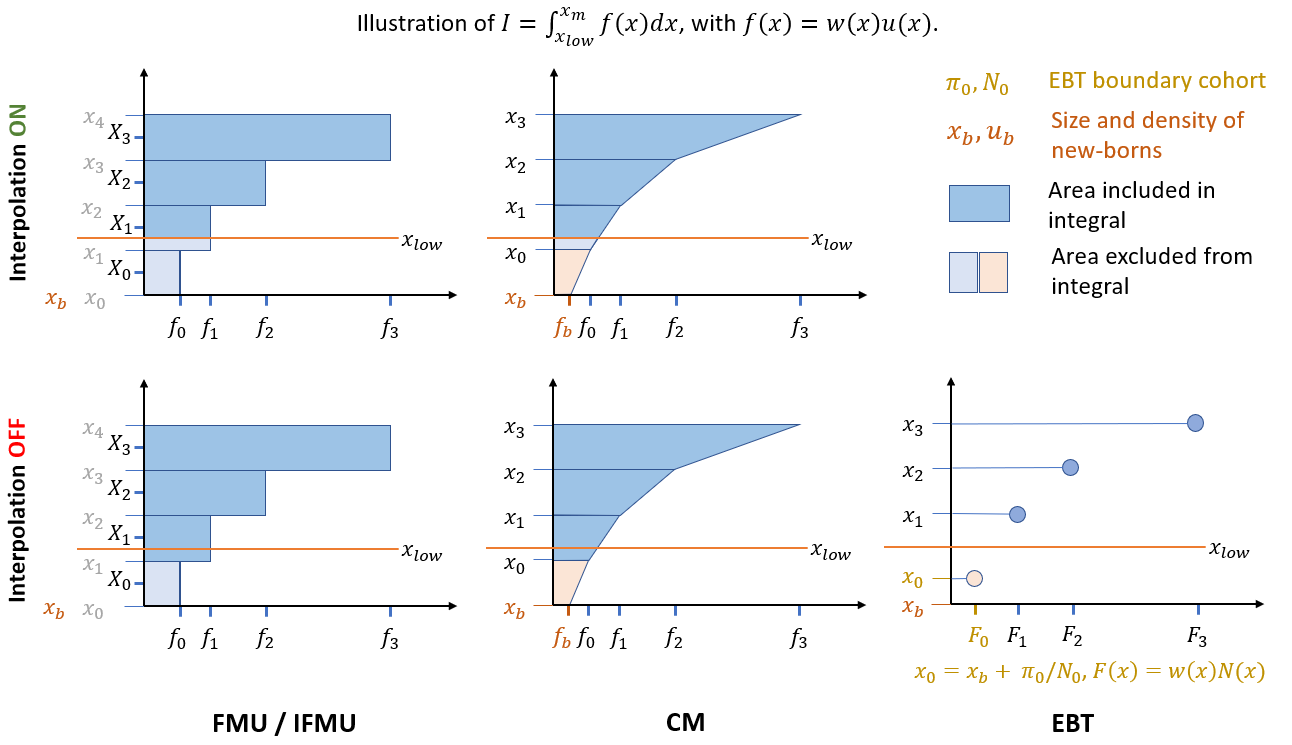
In libpspm, the computation of this integral depends on the solver method. For different solvers, the integral is defined as follows:

FMU: \(\quad I = \sum_{i=i_0}^J h_i w_i u_i\)

EBT: \(\quad I = \sum_{i=i_0}^J w_i N_i\), with \(x_0 = x_b + \pi_0/N_0\)

CM : \(\quad I = \sum_{i=i_0}^J h_i (w_{i+1}u_{i+1}+w_i u_i)/2\)

where \(i_0 = \text{argmax}(x_i \le x_{low})\), \(h_i = x_{i+1}-x_i\), and \(w_i = w(x_i)\).

If interpolation is turned on, \(h_{i_0}=x_{i_0+1}-x_{low}\), whereas \(u(x_{low})\) is set to \(u(x_{i_0})\) in FMU and calculated by bilinear interpolation in CM (See Figure). Interpolation does not play a role in EBT.

In the CM method, the density of the boundary cohort is obtained from the boundary condition of the PDE: \(u_b=B/g(x_b)\), where \(B\) is the input flux of newborns. In the current implementation of the CM method, \(B\) must be set to a constant. In future implementations which may allow real-time calculation of \(B\), \(u_b\) must be calculated recurvisely by solving \(u_b = B(u_b)/g(x_b)\), where \(B(u_b) = \int_{x_b}^{x_m} f(x)u(x)dx\).